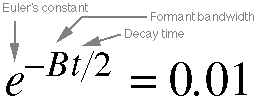
Equation 10.1. This equation calculates the time it takes for formant energy (from the singers' formant, at around 2800-3000 Hz) to 'die out', which for our purposes is assumed to be the time it takes for it to fade to 1% of its original loudness; thus the 0.01. B is the formant bandwidth in rad/s, and t is the decay time which we are solving for.

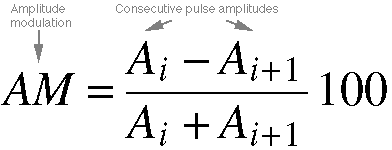
Equation 10.2. Here we are solving for amplitude modulation, the change in the deviation from equilibrium between two cycles of vocal fold vibration. We divide the difference between two back-to-back cycles by the sum, and then to get a percentage change, we multiply by 100.

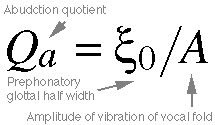
Equation 10.3. This equation is just simple division, but the variables could use some explanation. The abduction quotient is what we're solving for. The prephonatory glottal half width is the distance between the midpoint of the glottis and the center of either vocal fold when the folds are in a prephonatory position; i.e. as open as they get during the type of phonation being studied. A, the amplitude of vibration, is the distance between the midpoint of a vocal fold and the edge of the part in vi bration.

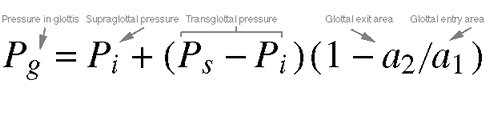
Equation 10.4: Mean aerodynamic driving pressure in the glottis. (Same as Equation 4.13) P_i is the pressure just above the glottis entering the vocal tract. The value a₂ over a₁, which is referred to as the glottal convergence ratio, varies from being near z ero when the folds are just starting to open (tiny space between the folds as they open means a small exit area), to near 1.0 just before the folds close. Since this value is multiplied by the transglottal pressure in our equation, this means that when th e glottal convergence ratio is near zero, it will tend to minimize the whole right side of the equation. However, when the convergence ratio is at its maximum, the transglottal pressure (P_s-P_i) will have more of an effect on t he pressure in the glottis, P_g.

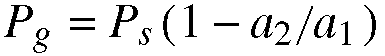
Equation 10.5.

This is a simplification of Equation 10.4; if we assume that P_i equals zero, we can drop the P_i terms out of the equation. Since P_i is the supraglottal pressure, which is affected by the vowel the sing ers is producing, this gives us an equation independent of vowel.

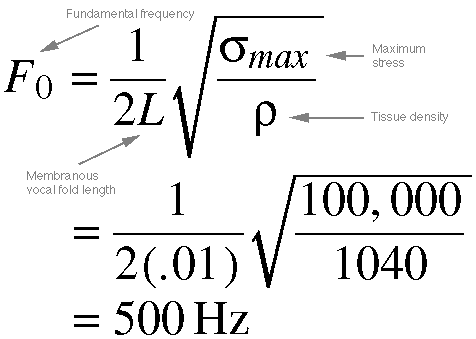
Equation 10.6. (Same as Equation 8-2) Here we try to predict where a register 'break' might occur based on known and assumed data about the human voice. The maximum TA activity is assumed to be 100 kPa (100,000 pascals), tissue density is 1040 kg/m³, and the length of the vocal fold in vibration is about 1 cm, which is .01 m. With these values plugged into our equation, we get a resulting F_o of about 500 Hz, which is right around C above middle C. This is about as high that a belter or trained classical tenor can pu sh his/her chest voice.