Chapter 8: Control of Fundamental Frequency

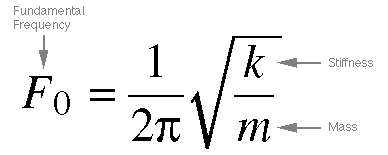
Equation 8.1. This equation derives the natural frequency of a simple mass-spring oscillator, of mass m and with a stiffness of k. The frequency is proportional to the square root of the ratio of stiffness to mass.

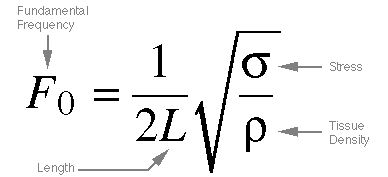
Equation 8.2. Similar to the first; it gives the natural frequency of an "ideal string", given its density, length, and the stress put on it.

However, determining the stiffness of vocal folds is rather more complex; they behave partly like strings and partly like springs. The following three equations help determine the effective stiffness of vocal folds:

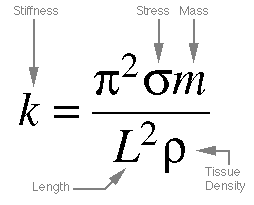
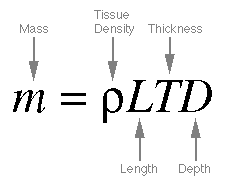
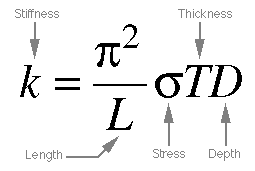
Equations 8-3, 8-4, and 8-5. Equation 8-3 is derived from 8-1 and 8-2, by equating the two fundamental frequencies (left sides of the equations), and then re-arranging remaining terms. 8-4 gives us the vocal fold mass, which is the amount of the vocal fold material that is effectively vibrating (the entire fold is not always in vibration). Finally, combining 8-3 and 8-4 gives us the effective stiffness, which is directly proportional to the vocal fold tension.

Equation 8.6: Vocal Fold Elongation. The length change in the vocal folds (strain) is given here. G, a gain factor, describes the range of stretching that can be achieved with CT and TA activity. R is a quantity which accounts for the mechanical advantage that the CT muscle has over the TA. The minus sign in the equation shows that the actions of the CT and TA are in opposition; the TA tries to shorten the folds, whereas the CT tries to lengthen them.

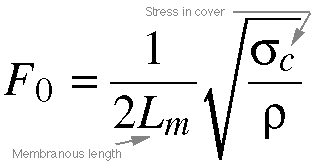
Equation 8.7. Here we have an equation to find the F_o of the cover of the vocal folds. It's identical to 8-2 above, except that the variables for stress and length are slightly renamed to show that it's just the cover we're talking about now, as opposed to the entire fold.

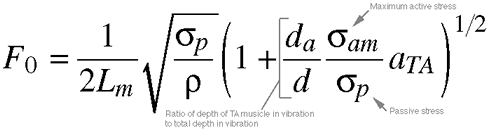
Equation 8.8. This last one gets a bit hairy, but if broken down into parts, it's not so bad. It's more complex because it takes into account a more sophisticated model of the vocal folds called the body-cover model. [It may also help to review the Body-Cover Model tutorial.] The simpler cover model is adequate to explain some frequency ranges and conditions, but it fails to account for the fact that TA muscle activity can both increase and decrease F_o. The reason for this is that part of the vocal fold body, the TA muscle itself, is vibrating when you produce low pitches or do especially loud singing.

Since the cover model accounts only for the cover and not the body, it makes sense that it would not explain situations involving activity in both the body and the cover. The entire part of the equation to the right of the square root sign is added in to account for TA activity. Note that if you set a_TA to 0, this part of the equation evaluates to 1 (zero times anything is zero, plus 1 is 1, and 1 to the 1/2 power is the square root of 1, which is also 1), and thus drops out entirely, leaving a n equation just like 8.7, the cover model equation.

The d_a/d part of the equation is the ratio of the depth of the TA muscle that is vibrating to the depth of all tissue that is vibrating, including the cover.

RHO_am/RHO_p is the ratio of the maximum stress that the TA can produce to the minimum stress produced by the TA when it is completely inactive, as it would be if paralyzed.