Chapter 4: Vocal Fold Oscillation

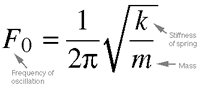
Equation 4.1. The frequency of oscillation, F₀, is the number of back-and-forth movements made per second. Since 1/2p₀ is a constant, and since the square roots of large numbers are larger than the square roots of smaller numbers, we can see that increasing the stiffness k will increase frequency, while increasing the mass m will decrease frequency.

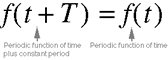
Equation 4.2. Here we have a mathematical definition of a periodic (i.e., repeating) waveform. If the waveform lasts for a pre-determined time T, then the waveform must be the same at the time t + T as it was at the time t. The quantity T is known as the period; it is the duration of one cycle of the waveform.

Simple Harmonic Motion: Equations 4-3 through 4-12

The next ten equations, which all lead up to 4-12, cover simple harmonic motion, also known as sinusoidal motion. The first four equations (4.3 through 4.6) are simple definitions of the trigonometric functions sine and cosine:

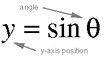
Equation 4.3.

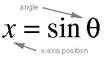
Equation 4.4.

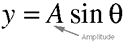
Equation 4.5.

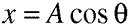
Equation 4.6.

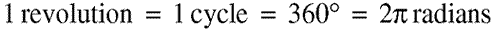
Equation 4.7. This equation makes clear the various ways in which circular motion can be expressed. Once around a circle is equal to all the quantities shown.

Equation 4.8. Frequency is the inverse of period. High-frequency oscillations have short periods, and vice versa.

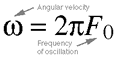
Equation 4.9. Oscillation can also be measure in terms of angular velocity, measured in radians per second. This is just a simple conversion; multiply F₀ by 2p to get the angular velocity in radians.

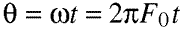
Equation 4.10. Here's the same expression, but now we're solving for the angle covered during a given period of time by the oscillation, in radians. We simply multiply the radian frequency by the elapsed time.

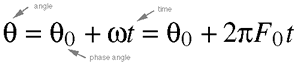
Equation 4.11.

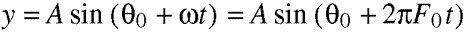
Equation 4.12. This is the general formula for simple harmonic, or sinusoidal, motion. As we can now see, there are three key quantities involved; the amplitude A, the phase q₀, and the frequency F₀.

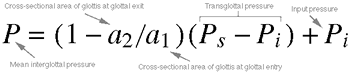
Equation 4.13. Here we are solving for the mean intraglottal pressure, which is the pressure inside the glottis over the medial surfaces of the vocal folds. You may refer to the Tutorial for Chapter 4 to see the quantities in this equation illustrated in an animated model.

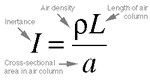
Equation 4.14. The inertance of an air column is defined as the air density times the length of the column, divided by its cross-sectional area.

Equation 4.15. This is Equation 4-14 written out in terms of Newton's second law of motion, which states that force = mass times acceleration. Force is analagous to the vocal tract input pressure, mass is analagous to inertance, and acceleration remains the same. If we restate this again with mathematics, we have:

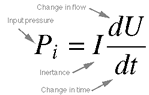
Equation 4.16. I is once again the inertance, dU/dt is the rate of change of the flow of air in the air column, and P_i, which we are solving for here, is the input pressure to the vocal tract. From this, we can see that the input pressure will be positive if the glottis is opening and the rate of change of the flow (acceleration) is positive.

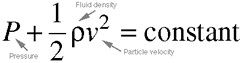
Equation 4.17: Bernoulli's energy law.   Refer to Equation 3-6.