Models of Vocal Fold Oscillation
What is oscillation?
Oscillation is a repeated back-and-forth movement.
Many common objects will oscillate for a short period of time
if set into vibration by being struck; bells, crystal glasses,
and so forth. What makes vocal fold oscillation more interesting
than a simple oscillator - such as a clock's pendulum - is
the question of how the back-and-forth movement can be sustained
over time. This phenomenon is called flow-induced oscillation.
A steady stream of air passing by a wall or surface can cause
that surface to vibrate; this can be seen in the way airplane
wings vibrate in flight, and in the rattling of air ducts in
heating systems.
As is the case for most scientific phenomena, vocal fold vibration was initially
explained with a somewhat simple - and as we will see, incomplete - model.
As more and more has become known about human phonation, subsequent models
have evolved in complexity. One of the first simple explanations of vocal fold
vibration relied on basic physical laws, particularly the Bernoulli effect,
the same effect that describes the 'lift' on an airplane wing. Over the past
few decades, scientists have increasingly had the benefit of computer systems
to create complex models to mimic vocal fold oscillation.
Myoelastic Aerodynamic Theory of Phonation
(Note: a full treatment of this topic is coverd in Dr. Ingo Titze's textbook with the same title. Link to NCVS book Sales).
Early voice researchers in the 1950's and 1960's explained vocal fold oscillation
with the myoelastic-aerodynamic theory. According to these theories,
Bernoulli forces (negative pressure) cause the vocal folds to be sucked together,
creating a closed airspace below the glottis. Continued air pressure from
the lungs builds up underneath the closed folds. Once this pressure becomes
high enough, the folds are blown outward, thus opening the glottis and releasing
a single 'puff' of air.
The lateral movement of the vocal folds continues until the natural elasticity
of the tissue takes over, and the vocal folds move back to their original,
closed position. Then, the cycle begins again. Each cycle produces a single
small puff of air; the sound of the human voice is nothing more than tens or
hundreds of these small puffs of air being released every second and filtered
by the vocal tract.
Let's further examine the myoelastic-aerodynamic theory. Myo- means
muscle; the vocal folds, after all, are mostly comprised of muscle tissue.
The -elastic suffix serves to remind us that the vocal fold is elastic
and that we have active control over its elastic properties. Aerodynamic means
that the theory deals with the motion of air and other gaseous fluids, and
with the forces active on bodies in motion (such as the vocal folds) in relation
to such fluids.
A depiction of this simple system is shown below:
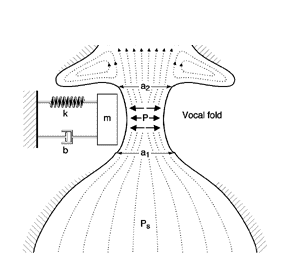
A simple rectangular block represents one vocal fold. A spring is useful
for portraying the tissue stiffness or restoring force in the vocal fold. Finally,
we've added a damping constant to represent the viscosity (energy absorption)
of the tissue. The damping constant is similar to the shock absorber on a car
or a tubular damper on a screen door.
So, how well does this simple model explain how the vocal folds sustain oscillation?
Not well at all, researchers have found. Bernoulli forces alone cannot account
for continual energy conversion from airstream to tissue. Soon, oscillation
would damp out.
The One-Mass Model
A crucial component must be added to our simple model. An acoustic tube (to
represent the vocal tract) is now attached to our model. Why is the acoustic
tube needed? For the vocal folds to sustain oscillation, we know there must
be a negative pressure within the glottis. But, pressure from the lungs cannot
be negative; it is always positive. So, how does the air pressure at the
level of the glottis become negative? Make a mental image of the the air
from the lungs moving uni-directionally upward. When the glottis is closing,
the airflow begins to decrease, but the air that is above the glottis does
not "know" this, so it continues to move with its same speed (because of
inertia). This creates a region just above the vocal folds where the air
pressure decreases, because air is not coming from the bottom through the
glottis as fast as it is leaving above. When the vocal folds are opening,
fluid pressure against the walls is greater than when the vocal folds are
close together. Thus, it is the asymmetry of driving force (air) that sustains
oscillation.
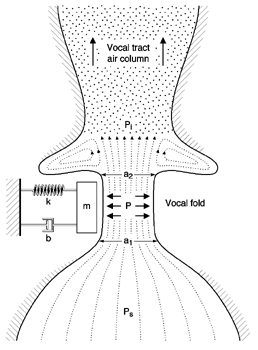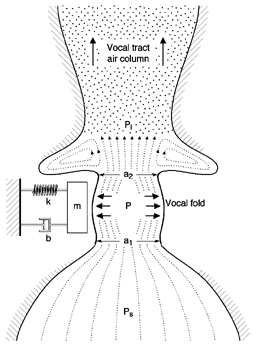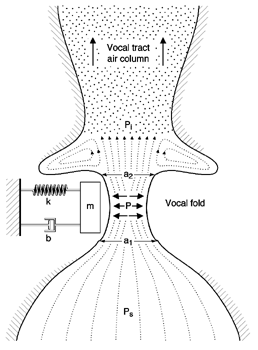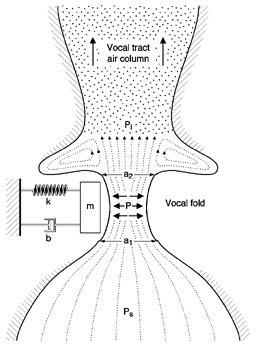
Although our one-mass model is a closer representation of actual vocal fold
oscillation than the myoelastic-aerodynamic model, some refinements will make
the model even more like human phonation.
An increased use of videostroboscopy in clinics and research labs has allowed
vocologists to observe many sets of vocal folds in slow motion. These observations
have shown that vocal folds rarely move in a uniform block as depicted in our
one-mass model. Rather, the vocal folds move in a wave-like motion from bottom
to top, with the bottom edge leading the way. A more sophisticated version
of the model can mimic the motion.
The Three-Mass Model
So, let's continue building our model. In order to model the shape of the vocal
folds more accurately, we add two small masses (depicted as m1 and m2),
one on top of the other, to represent the cover of the vocal fold. A large
mass (depicted as m) represents the thyroarytenoid muscle. Although
independent of one another in movement, all three masses are connected by
springs and damping constants. Here is how the model looks and moves now:
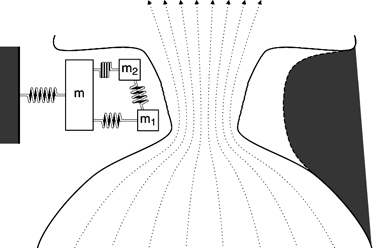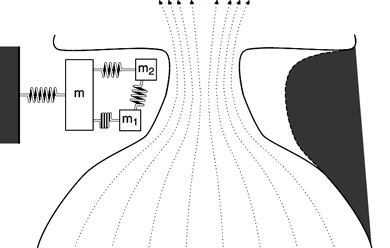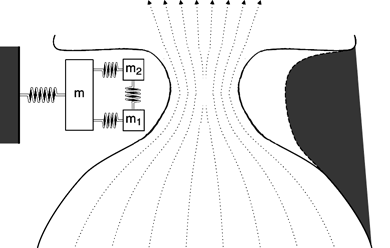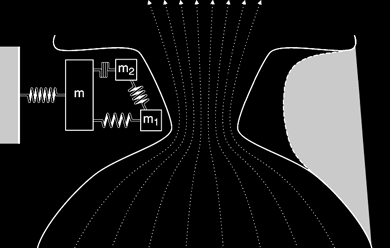
Note that at some points in the cycle, the bottom of the vocal folds are
farther apart than the upper part of the folds. We call this a convergent shape
because the airflow is converging. On the other hand, the airflow diverges
when the lowermost parts of the vocal folds are closer together; this is a
divergent glottal shape. Average air pressures within the glottis tend to be
larger in the convergent glottal configuration than in the divergent shape,
resulting in the asymmetry of air pressures needed to sustain oscillation.
As technical capabilities in computer software and hardware increase and
as improved imaging techniques allow researchers to study vocal folds in motion,
models are increasingly becoming more realistic. Dr. Ingo Titze and his colleagues
at The University of Iowa routinely use 16-mass models in their studies.
Tutorials Homepage
|



