Chapter 5: Generation and Propogation of Sound

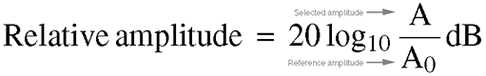
Equation 5.1. This equation determines the relative amplitude, in decibels, that a given sound A has compared to a reference sound A₀. We use the reference sound since decibels are only a relative measure of 'loudness', and not an absolute measure.

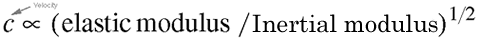
Equation 5.2. The speed of sound, c, varies according to the medium the sound is traveling through. Specifically, from Equation 4.1, we know that the frequency of a mass-spring oscillator is proportion to the square root of the ratio of stiffness to mass. If the medium is stiffer when compressed, the sound waves will travel (propagate) faster. If the medium is more stretchy and elastic, waves will travel slower through it. The mass we are concerned with is not the total mass of the medium, but its density, or mass per unit volume. The greater the density of the surrounding medium (usually air, for our purposes), the slower sound will propogate through it. The elastic modulus refers to stiffness, and the inertial modulus refers to density.

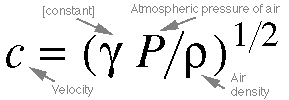
Equation 5.3. This is a more specific version of Equation 5.2. P, the atmospheric pressure of the surrounding air, is substituted in for the elastic modulus, and the air density is substituted for the inertial modulus.

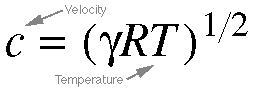
Equation 5.4. Equation 2.10 tells us that for a gas, pressure and volume are inversely proportional. Also, pressure is directly proportional to temperature. Plugging those concepts into Equation 5.3 gives us this equation. Temperature is relevant here, because the vocal tract is generally warmer than the average outside temperature. The speed of sound is about 350 m/s in the vocal tract, as opposed to 343 m/s under average atmospheric conditions.

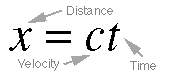
Equation 5.5.

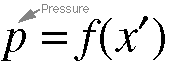
Equation 5.6.

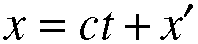
Equation 5.7.

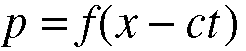
Equation 5.8.

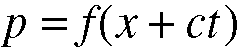
Equation 5.9.

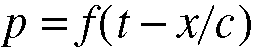
Equation 5.10.

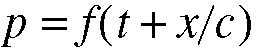
Equation 5.11.
The above seven equations all deal with the motion of a wave through space and time, so we will deal with them together. 5.5 simply states that an object traveling at a velocity c will travel a distance x during a period of time t. Sound waves aren't objects, of course, but we can treat them as such for our purposes. 5.6 defines the pressure p in terms of an arbitrary function f. This function could be a sine wave, a bell curve, or whatever shape that describes the disturbance in air pressure that the sound wave causes at a given moment. The variable x' is the distance from the peak of the wave. In 5.7, we calculate the distance from the origin of the wave to the peak of the wave. Now if x = ct + x', then x' = x - ct; we can see this from simple subtraction. And since 5.6 tells us that p = f(x'), we can simply substitute in x - ct in place of x'. This is done in Equation 5.8. The last three equations, (5.9 thru 5.11), are restatements of 5.8, given here and in the book to show that reversal of the sign or the order of the variables does not alter the fundamental properties of the wave as it moves through a medium.

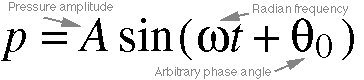
Equation 5.12: Sinusoidal Waves. The formula for determining the pressure variation, p, of a sinusoid is given here. The phase angle Q₀ determines the time at which the sinusoid reaches its peak. The peak of our wave travels at a velocity c, and so we know that for our wave to travel a given distance x, it will take an amount of time x/c. This leads to the next equation...

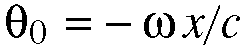
Equation 5.13. This is the phase angle. Substituting this into 5.12 for the Q₀ term gives us the next equation.

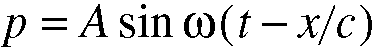
Equation 5.14. This describes a sinusoidal pressure wave moving to the right, also known as a forward wave. This is just a fleshed out version of Equation 5.8, with the generic function f replaced with a real function -- that of a sinusoid. If the sinusoid were traveling backwards, there would be a + sign in the parentheses instead.

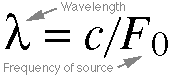
Equation 5.15: Wavelength. Wavelength is the distance between successive iterations of a wave. For a simple sinusoid, it's the distance between each peak in pressure; each 'hump' in the wave. Wavelength is determined both by the frequency of the source and by the medium. High-frequency sources, for instance, produce many pressure peaks per second, and since the velocity of those peaks (the speed of sound) is fixed and determined by the medium, the peaks will be relatively close together. Low-frequency sources will generate peaks which are further apart. Our equation states that wavelength is the speed of sound divided by frequency. The next two equations are derived from 5.14 and 5.15 by substitution:

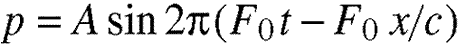
Equation 5.16.

Equation 5.17.

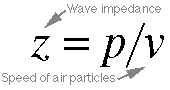
Equation 5.18: Wave Impedance. Wave impendance is the ratio of pressure to the speed of the air particles being pushed by that pressure. Wave impedance is also related to the speed of sound, as we see in the next equation:

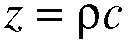
Equation 5.19. Here, we see that wave impedance is equal to r, which is the air density, multiplied by c, the speed of sound.

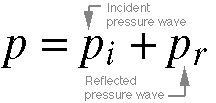
Equation 5.20. Our last three equations for this section govern reflections of sound. The total pressure p in 5.20 is the sum of p_i, the incident pressure (the pressure which is hitting the surface that the wave is reflecting from), and p_r, which is the pressure that is reflected back from the surface.

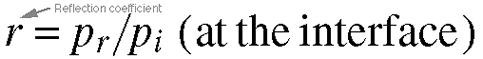
Equation 5.21. In real life, the surfaces which sound reflects from are not perfectly stiff; they do not reflect back all of the energy directed at them. The reflection coefficient tells us how much energy survived the collision and got reflected. It is derived simply by dividing the reflected energy by the original energy that the wave possessed.

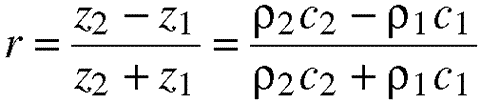
Equation 5.22. Here, Equation 5.21 is re-stated in terms of wave impedances, as defined above in 5.18 and 5.19.