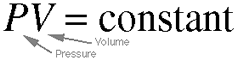
Equation 3.1: Boyle's Law This is a simpler re-writing of Equation 2.11, which is the ideal gas law with the right side set to a constant. It states that given a soft-walled enclosure with a constant temperature, pressure and volume are inversely related; increasing one causes a proportional decrease in the other. This law explains why our lung pressure decreases when we increase the lung volume by expanding the rib cage and contracting the diaphragm.

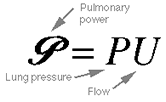
Equation 3.2. Pulmonary power is the product of lung pressure and flow. In speech and singing, the power being delivered through the glottis by airflow can vary by a factor of at least 100 times! The approximate maximum power a human can deliver is one watt, as given by the equation below:

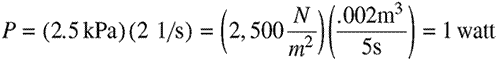
Equation 3.3. This simply uses Equation 3.2 above and some assumptions of human lung pressure and flow rates to arrive at the 1 watt estimate.

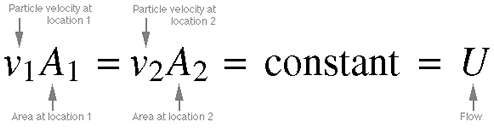
Equation 3.4: Continuity Law of Incompressible Flow. Assuming that airflow is confined in a duct or pipe, and that density does not change when the air travels through a constricted space (i.e. the air cannot be compressed), this law dictates that the speed of the air must increase as it travels through the constriction, in order to make up for the smaller space.

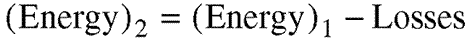
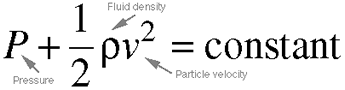
Equations 3.5 and 3.6: Bernoulli's Law (Conservation of Energy). Since the pressure and the particle velocity are on the same side of this equation and are added to result in a constant, and since fluid density does not change, we can see from this law that if the particle velocity increases, like it would in a constriction, the pressure must decrease, which seems counterintuitive, but is true anyway. That's life for you.

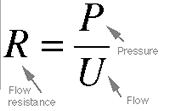
Equation 3.7.   R, resistance, is given as the ratio of pressure to flow. This ratio is different for different constrictions in the vocal tract, such as the glottis itself, or the small space between your tongue and teeth when you produce an [s] sound.

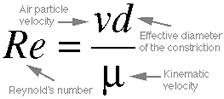
Equation 3.8. This equation defines Reynold's number, which helps to characterize how flow will behave through various constrictions. Fluid mechanics engineers have discovered that when this number is larger than a critical value, flow tends to be turbulent, i.e., it basically sprays all over the place chaotically after exiting from the constricted space, like a garden hose with the end covered mostly by your thumb. But if Reynold's number is smaller than the critical amount, the flow is laminar, or smooth, like an open garden hose.